算数にはいろいろな解法があるのが面白い。いくつも別解があるものを取り上げてみました。また、家庭教師として重要なのが、生徒の多様な解き方をまず理解することです。
差集めか比か 受験算数別解集
ひとつの問題を中学受験の12通りの解法で解く
【問題】
平らな正方形の土地に支柱を立ててサクを設置し、牧草地にして牛と話すことにしました。
支柱を何メートルおきに立てるかを決めるため、まずは正方形の土地の一辺のためだけに使う支柱を準備しました。一辺の端から端まで、支柱を5mおきに立てようとしたところ37本不足しました。また、8mおきに立てたら23本余りました。支柱を何本用意したかを答えなさい。(北嶺中算数 2015平成27年)

設問のまとめ
●ある区間(土地の一辺)に準備してある支柱を立てる。
●5mおきだと支柱は37本不足
●8mおきだと支柱は23本余る
●準備した支柱の数を求める出題(区間の長さも不明)
設問の文面を見ると、「不足しました、余りました」とあるのが目に入るので、まずは、差集め・過不足算系の問題かと考えるだろう。
なにはともあれ、図を書いてみよう。

【解法1 過不足算】
うーん。37本と23本をどう使うのか。とりあえず、これらも並べてみると、下の図のようになる。
「37本不足」というのは5mおきに並べるのが前提だし、8mの余った分も8mおきに並べてみる。

並べることで、本数と距離とが別の次元であることに気づく。ここで混乱すると、距離と本数を足し算するような式を作ってしまう。
その原因
過不足算典型題「お菓子を皿に5個ずつ配ると○〇個足りず、8個づつだと○〇個不足する」では
お菓子の個数で比べる。
だがここではそうではない。今は本数ではなく距離の式を作ろうとしている。
過不足算応用題「お菓子をひと皿5個ずつ配ると37皿分足りず、8個づつだと23皿分不足する」
余ったり不足するのが(個数ではなく)何人分(何皿)である。
皿数×1皿の個数=「総個数」
同じことで
間隔数×(支柱の1間隔分5mまたは8m)=「距離」
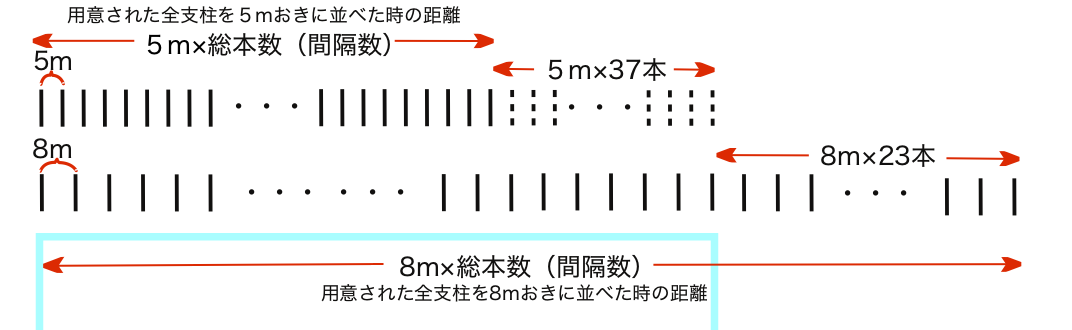
また、 植木算は間隔の数で計算する。
上の図を書くと、一番左の1本を除くと、間隔=1本を除いた本数、とわかるし、37本と23本の区間もそれぞれ37間隔、23間隔で計算できることがわかる。一番左の一本を最後に加えればいい。
【線分図】
ここで、8mおきに全部並べた時と、5mおきに全部並べた時の差、全体の差は赤字の部分(8-5)×間隔数で、図より(37×5)+(23×8)mと等しくなる。 上の図を手早く線分図で書くという定石がある。

各間隔を3mずつ延ばして全体の差になるのだから、
間隔数=(5×37+8×23)÷3
間隔数=123、よって植木算の1を加え支柱の本数は124本
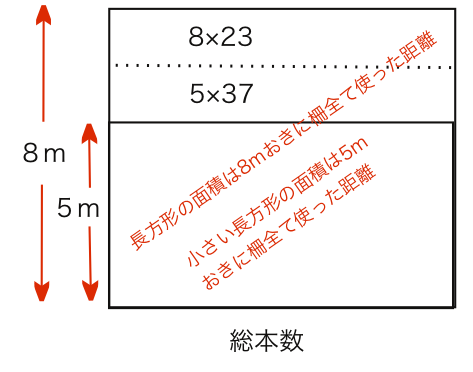
【面積図】
過不足算で面積図を使うのはいまいちな気がするが、掛け算になるものは面積図のほうがわかりよい場合があろう。
長方形の面積は縦×横(間隔の距離×間隔の数=すべての距離)で表される。江戸時代から使われてきた。
【方程式】
差集め算は中学校で方程式の単元でも習うが、結構難度が高い。図を書かないとプラスとマイナスを取り違えたりしそうだ。しかし、方程式的な式の感覚で解くのは中学受験の小学生にとっても役に立つことがあるといえる。
(総本数ー1)の間隔数をⅩとおき区間の長さ(土地の一辺)についての等式であらわすと
5×(Ⅹ+37)=8×(Ⅹー23)
これを展開したのが上と同じ式
5×Ⅹ+5×37=8×Ⅹー8×23
【差集めの図】
昔から有名な典型題「長椅子に5人ずつ座ったら、席が37席不足した、また8人ずつ座ったら23席余った。」
くらべてみると、8人ずつ座ると席が余り、5人ずつだと不足するはずなので、今回の柵の問題(8mずつだと23本余り、5mづつだと37本不足)とちょうど同じになる。また、今回は「最後の椅子には2人だけが座る」というような「端数」「あまり」が出現してないのもポイント。もし、端数があったら、面積図や線分図もめんどくさいことになる。ここで、端数がでても対応できる原始的な「絵」で書く解法。
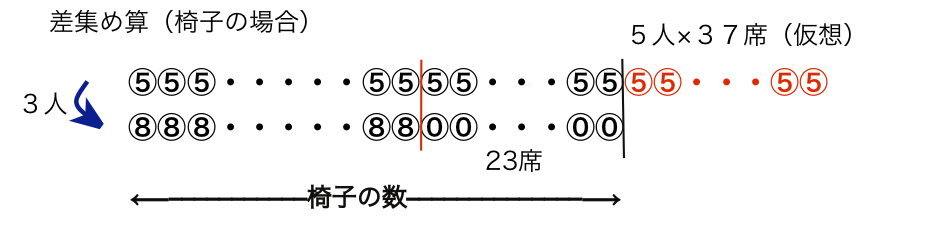
赤線より左の各3人の差が集まって赤線より右の5人×(23+37)席となるので、(23+37)×5÷3 が赤線左の8人が座っている席数、これに23を加えると答え123席とわかる。そして、今回の柵の問題の場合は植木算の1を加える。
※これは実は下の「共通積の面積図」と同じものであり解法2の考え方といえる。
【解法2 差集め算、視点を変えて】
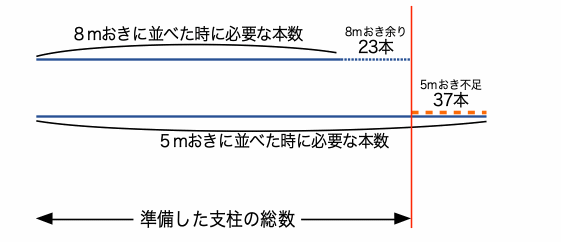
●解法1は距離の次元で考えたが、それと違って、本数だけを考えて線分図を書くと下の図のようになる。8mおきの方が使用する支柱の数が少ないので線分は短くなる。
●5m区間の「足りない」支柱は見えないではないか、と感じるかもしれないが、下の図を書けば、想定として意味があるので、数にいれる。
【差集算、積が共通の面積図】
典型題「池の周りにクイを打ちます。5mおきに打つのと8mおきに打つのでは60本の差があります」
解法1の面積図とは違って、現在ある総本数ではなく、上の線分図の「必要な本数」で考える。やはり面積は距離を表すが、共通の距離(池の周り、区間の長さ)が前提としてあることに気づく。
5mおきと8mおきに支柱をこの区間にそれぞれ並べた場合、支柱の数の差は37+23の60間隔分である。
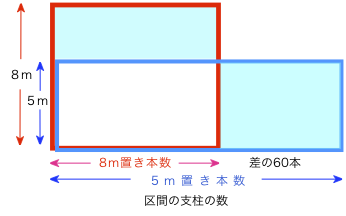
赤青2つの長方形の面積は
「支柱1間隔あたりの距離(縦)×支柱の本(間隔)数(横)」
=区間の距離(土地の一辺)。
だから、同じ面積。(積が共通)
ということは、水色の部分も同じ面積。まず分かるのは右下 5m×60本。
つまり右下5×60=左上(8−5)×口(8mおき本数)
より 口=100
8mおきだと100間隔、5mおきだと160間隔と分かる。
2数を掛けた8×100、5×160いずれも800m(区間の長さ)
よって、100間隔+23余りまたは160間隔-37不足分の答えいずれも123間隔に植木算の1を加えて答124本
【解法3 逆比・反比例】
●同じ長さの区間では、支柱1か所あたりの間隔を2倍長くとれば、柱の(間隔)数は1/2となる。3倍でも4倍でも同様。
(目盛りのある線分図で二つ分の目盛りをとると、とる数は半分になる。または、1間隔の長さ×間隔の数=全体の区間の長さ、だから)
【逆比】
5m置きと8m置きでは、同じ長さの区間だと、使う支柱の(間の)数は逆比なので(反比例していて)、1/5:1/8=8:5となる。
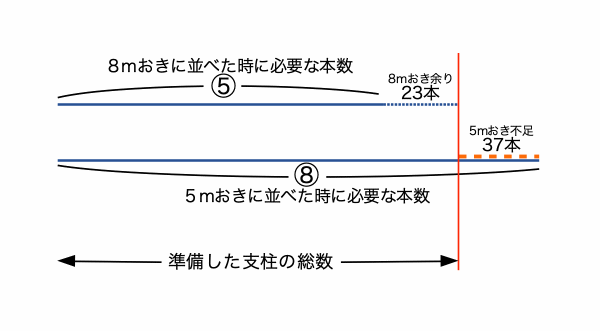
そして、数の差が60本(23+37)である。
ということは、上の図から⑧-⑤=③が60本にあたるので、比の①は20本、だから比の⑧(5mおきの場合)は160本、比の⑤(8m置きの場合)は100本となる。(区間の長さは5×160=8×100=800m。)
よって、100+23または160-37の答え123間隔に一番端の柵の1を加えて答124本
※逆比の説明。区間の長さを仮に40と固定すると、5m置きは8本(間隔)使い、8m置きは5本使うから。8×5=5×8、一方が2倍3倍になれば、もう一方は1/2、1/3になる。反比例(逆比例)しているを省略して逆比と呼ぶ。5:8の逆比は1/5:1/8=8:5 これは解法2の面積図でもあり、食塩水天びん法などでも使われる。
【反比例の公式から】
支柱間隔が2倍、3倍になれば、支柱の間隔数は1/2、1/3となる。
1間隔×間隔数=区間の長さ、つまり「積が一定」で、1間隔と間隔数が反比例している。この「積が一定の定数をa(一辺の長さは未知だが決まっているので定数)」とおく反比例の公式
xy=aで(掛け算の×記号を省略すると大人っぽく見えるぞ)、aが40ではなく未知の土地の一辺の距離(m)、x、yは変数でxをそれぞれの1間隔(m)、yを(8mおきの)間隔数(本)とおくと
5(y+60)=8y=a
のような式になる。この方程式を面積図にしたものが、解法2の「共通積の面積図」になり、同じ面積の長方形の右上の点が反比例のグラフ双曲線の一部でもある。
【相当算・倍数算の比例式】
この同じ区間に、5mおきだと「総本(間隔)数+37本」が並び、8mおきだと「総本数ー23本」が並んでいることになる。
総本数を①とおくと、下の図より(逆比を利用)
(①+37):(①-23)=8:5
⑤+5×37=⑧ー8×23
さあ消去算・逆算の腕だめしだ。まず両天秤から⑤を引く。
③=369
①=123
総本数が出るので、これに左端の1を加えると答え124本
【解法4 公倍数・1とおく】
【公倍数】
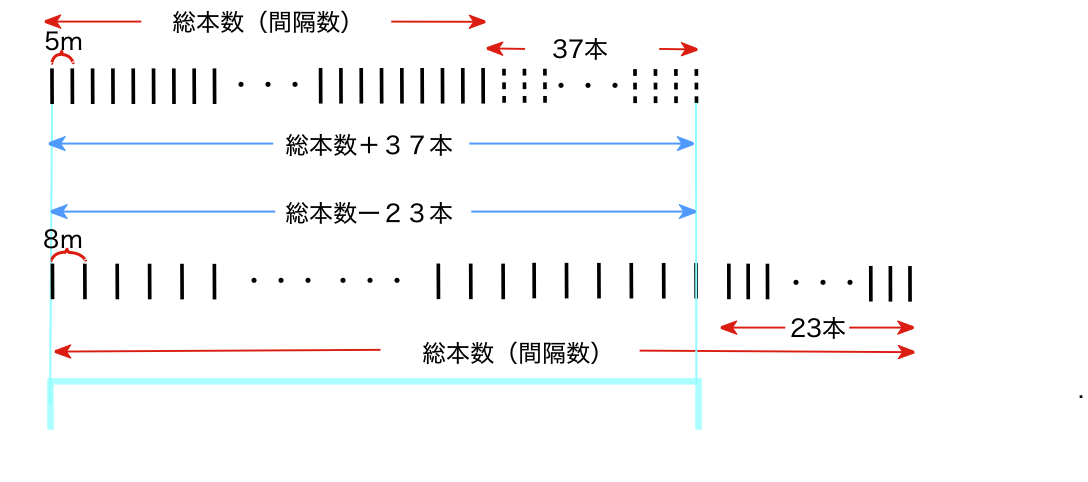
端から端まで支柱が立つというのだから、区間の左端と右端に支柱が立つ(たとえば20㎝余ったなどの端数がない)。下の図のように公倍数40mごとに支柱が重なるので、これがぴったり敷き詰められ、区間の長さは40の倍数である。
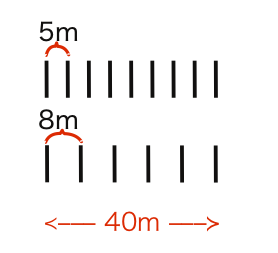
この40メートルの1セット内で上の5m区間は8つあり、下の8mは5つあるから、間膈数の差は8間隔ー5間隔=3間隔である。
全体の本数の差は37+23の60間隔差であった。だから、区間は60÷3の20セット分、800mとなる。
800m÷8mおき=100間隔
800m÷5m=160間隔
100間隔+23間隔=160間隔ー37間隔=123間隔
123間隔+1本=124本
【全体を1とおく 仕事算?】
区間の長さ(土地の一辺)を1とおくと支柱の間隔数は5mおき、8mおきそれぞれ1÷5、1÷8(1の中に5m、8mが何か所あるか)だから 1/5か所、1/8か所。(1じゃなくて40とおけば、40の中に5mは40÷5で8か所、8mは40÷8の5か所となりわかりやすいか。上の公倍数の図を参照。)
60:(1/5-1/8)=x:1(小6で習う比を使う場合)
60 ÷( 1/5 ー 1/8 )=800
以下同文。
「1とおく」のは割り算の意味の理解を習う小学校5年の「学校指導の範囲」であり中学受験独特の方法を避ける場合に多用されると思うのだが、これがなかなか難しい。
【解法5 比例のグラフ 速さと比】
とくに解法2・3では、目に見えない柵も含めての差を考えるという点で、理解しにくい場合があるかもしれない。2つの次元をまとめる目的といえばグラフだ。何m置きでも「本数」と「距離」は単純な掛け算でグラフが直線(本数なので実は整数のみだが)で、5mおきと8mおきの二本の比例をあらわすグラフ。縦の次元が解法1であり、横に切った次元が解法2・3である。
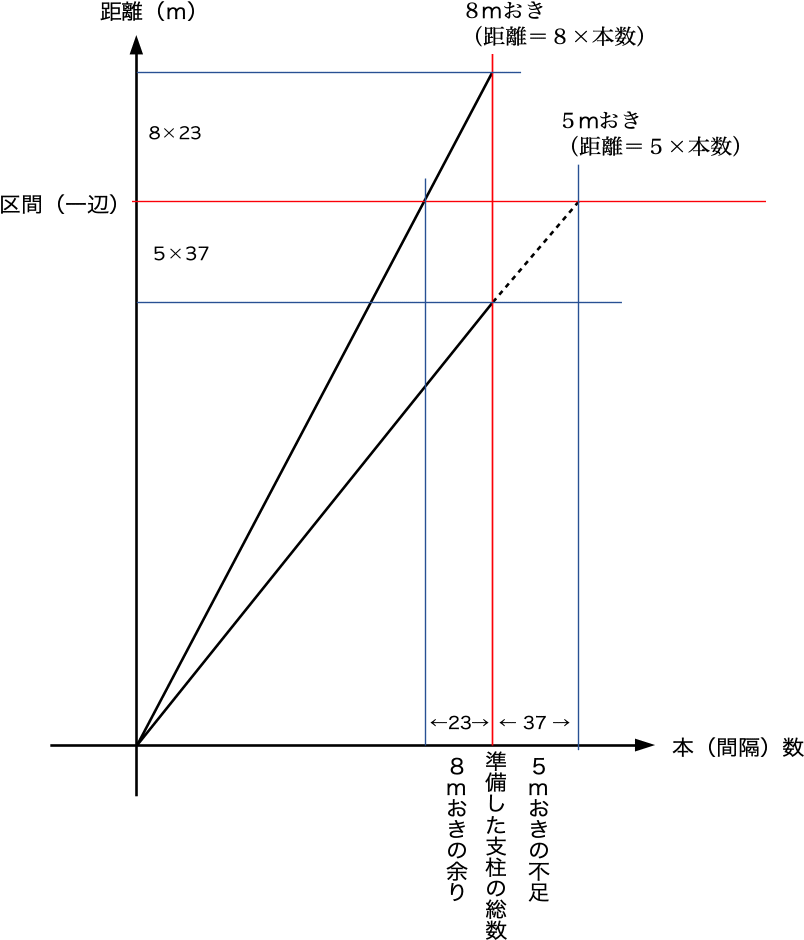
典型題「兄と妹の速さの比が8:5の時、同時に出発して兄は定刻の23分前に到着したが妹は37分遅刻した。」
「速さと比」と同じことで、距離が等しい時、速さが5:8ならば、かかる時間は 1/5:1/8 つまり8:5になる。今回はこの差の③が60本(60分)だと判明していることになる。